Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)
The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) adalah metode analisis keputusan multi-kriteria, yang pada awalnya dikembangkan oleh Ching-Lai Hwang dan Yoon pada tahun 1981 dengan perkembangan lebih lanjut oleh Yoon pada tahun 1987, dan Hwang, Lai dan Liu pada tahun 1993. TOPSIS didasarkan pada konsep bahwa alternatif yang dipilih harus memiliki jarak geometris terpendek dari solusi ideal positif (SIP) dan jarak geometris terpanjang dari solusi ideal negatif (SIN).
Daftar Isi
- Metode TOPSIS
- Contoh Kasus Perihtungan TOPSIS
- Perhitungan TOPSIS dengan Excel
- Database TOPSIS
- Source Code TOPSIS
Metode TOPSIS
Langkah 1: Matriks Evaluasi
Buat matriks evaluasi yang terdiri dari m alternatif dan n kriteria, dengan perpotongan setiap alternatif dan kriteria yang diberikan sebagai \(x_{ij}\), oleh karena itu kita memiliki matriks \((x_{ij})_{mxn}\).
Langkah 2: Normalisasi
Matriks \((x_{ij})_{mxn}\) kemudian dinormalisasikan menjadi matriks
\(R=(r_{ij})_{mxn}\) menggunakan metode normalisasi
\( r_{ij} =\frac{x_{ij}}{\sum_{k=1}^{m}}x^2_{kj}, \: \: \: i=1, 2, 3, m, \: \: \: j=1,2,3,n \)
Langkah 3: Normalisasi Terbobot
Hitung matriks keputusan ternormalisasi berbobot
\( t_{ij}=r_{ij}.w_j, \: \: \: 1, 2, ..., m, \: \: \: 1, 2, ..., n \)
Dimana \( W_j=\sum_{k=1}^{n}W_k, j=1,2,...,n \) sehingga \( \sum_{i=1}^{n}w_i=1 \) dan \( W_j \) adalah bobot asli yang diberikan terhadap kriteria \( v_j, j=1,2,...,n \)
Langkah 4: Solusi Ideal
Menentukan alternatif terburuk \( A_w \) dan alternatif terbaik \( A_b \):
$$ A_w=\left \{ \left \langle max(t_{ij}|i=1,2,..,m)|j\in J_- \right \rangle, \left \langle min(t_{ij}|i=1,2,..,m)|j\in J_+ \right \rangle \right \} \equiv \left \{ t_{wj}|j=1,2,...,n \right \} $$
$$ A_b=\left \{ \left \langle min(t_{ij}|i=1,2,..,m)|j\in J_- \right \rangle, \left \langle max(t_{ij}|i=1,2,..,m)|j\in J_+ \right \rangle \right \} \equiv \left \{ t_{bj}|j=1,2,...,n \right \} $$
dimana,
\( J_+= \left \{j=1,2,...,n \right \} \) untuk kriteria benefit
\( J_-= \left \{j=1,2,...,n \right \} \) untuk kriteria cost
Langkah 5: Jarak Solusi Ideal
Hitung jarak L2 antara alternatif target \( i \) dan kondisi terburuk \( A_w \)
$$ d_{iw}=\sqrt{\sum_{j=1}^{n}(t_{ij}-t_{wj})^2}, \: \: \: i=1,2,...,m, $$
dan jarak antara alternatif target \( i \) dan kondisi terbaik \( A_b \)
$$ d_{ib}=\sqrt{\sum_{j=1}^{n}(t_{ij}-t_{wb})^2}, \: \: \: i=1,2,...,m, $$
di mana \( d_{iw} \) dan \( d_{ib} \) adalah jarak normal L2 dari alternatif target \( i \) ke yang terburuk dan terbaik kondisi masing-masing.
Langkah 6: Nilai Preferensi
Hitung kesamaan dengan kondisi terburuk:
\( s_{iw}=d_{iw}/(d_{iw}+d_{ib}), \: \: \: 0 \leq s_{iw} \leq 1, \: \: \: i=1,2,...,m. \)
\( s_{iw}=1 \) jika dan hanya jika solusi alternatif memiliki kondisi terbaik; dan
\( s_{iw}=0 \) jika dan hanya jika solusi alternatif memiliki kondisi terburuk.
Langkah 7: Perangkingan
Beri peringkat berdasarkan \( s_{iw} (i=1,2,...,m) \).
Contoh Kasus Perhitungan TOPSIS
#01 Matriks Evaluasi
Berikut adalah contoh data penilaian alternatif untuk masing-masing kriteria.
| Kode | Nama | Tanggungan | IPK | Semester | Penghasilan Orang Tua |
|---|---|---|---|---|---|
| A1 | Maria | 5 | 3 | 3 | 2 |
| A2 | Ana | 5 | 5 | 3 | 5 |
| A3 | Antonio | 1 | 2 | 3 | 1 |
| A4 | Thomas | 3 | 3 | 1 | 3 |
| A5 | Christina | 4 | 5 | 3 | 2 |
Data kriteria ada empat sebagai berikut.
| Kode | Nama | Atribut | Bobot |
|---|---|---|---|
| C1 | Tanggungan | benefit | 3 |
| C2 | IPK | benefit | 2 |
| C3 | Semester | benefit | 2 |
| C4 | Penghasilan Orang Tua | cost | 3 |
#02 Normalisasi
Tahap pertama normalisasi adalah mengkuadratkan masing-masing nilai matriks \( x_{ij} \)
| Kode | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| A1 | 5*5=25 |
3*3=9 |
3*3=9 |
2*2=4 |
| A2 | 5*5=25 |
5*5=25 |
3*3=9 |
5*5=25 |
| A3 | 1*1=1 |
2*2=4 |
3*3=9 |
1*1=1 |
| A4 | 3*3=9 |
3*3=9 |
1*1=1 |
3*3=9 |
| A5 | 4*4=16 |
5*5=25 |
3*3=9 |
2*2=4 |
Tahap kedua normalisasi adalah mencari akar dari total nilai kuadrat setiap kriteria.
| Kode | Perhitungan | Hasil |
|---|---|---|
| C1 | \( \sqrt{25+25+1+9+16} \) | 8.7178 |
| C2 | \( \sqrt{9+25+4+9+25} \) | 8.4853 |
| C3 | \( \sqrt{9+9+9+1+9} \) | 6.0828 |
| C4 | \( \sqrt{4+25+1+9+4} \) | 6.5574 |
Tahap ketiga normalisasi adalah membagi setiap elemen matriks \( x_{ij} \) dengan hasil tabel di atas.
| Kode | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| A1 | 5 / 8.7178 = 0.5735 |
3 / 8.4853 = 0.3536 |
3 / 6.0828 = 0.4932 |
2 / 6.5574 = 0.305 |
| A2 | 5 / 8.7178 = 0.5735 |
5 / 8.4853 = 0.5893 |
3 / 6.0828 = 0.4932 |
5 / 6.5574 = 0.7625 |
| A3 | 1 / 8.7178 = 0.1147 |
2 / 8.4853 = 0.2357 |
3 / 6.0828 = 0.4932 |
1 / 6.5574 = 0.1525 |
| A4 | 3 / 8.7178 = 0.3441 |
3 / 8.4853 = 0.3536 |
1 / 6.0828 = 0.1644 |
3 / 6.5574 = 0.4575 |
| A5 | 4 / 8.7178 = 0.4588 |
5 / 8.4853 = 0.5893 |
3 / 6.0828 = 0.4932 |
2 / 6.5574 = 0.305 |
#03 Normalisasi Terbobot
Tahap pertama dalam menghitung normalisasi terbobot adalah dengan membagi masing-masing bobot kriteria dengan total bobot kriteria
| Kode | Perhitungan | Bobot |
|---|---|---|
| C1 | 3 / (3+2+2+3) | 0.3 |
| C2 | 2 / (3+2+2+3) | 0.2 |
| C3 | 2 / (3+2+2+3) | 0.2 |
| C4 | 3 / (3+2+2+3) | 0.3 |
Tahap kedua adalah mengalikan matriks normalisasi dengan bobot normal di atas.
| Kode | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| A1 | 0.5735 * 0.3 = 0.1721 |
0.3536 * 0.2 = 0.0707 |
0.4932 * 0.2 = 0.0986 |
0.305 * 0.3 = 0.0915 |
| A2 | 0.5735 * 0.3 = 0.1721 |
0.5893 * 0.2 = 0.1179 |
0.4932 * 0.2 = 0.0986 |
0.7625 * 0.3 = 0.2287 |
| A3 | 0.1147 * 0.3 = 0.0344 |
0.2357 * 0.2 = 0.0471 |
0.4932 * 0.2 = 0.0986 |
0.1525 * 0.3 = 0.0457 |
| A4 | 0.3441 * 0.3 = 0.1032 |
0.3536 * 0.2 = 0.0707 |
0.1644 * 0.2 = 0.0329 |
0.4575 * 0.3 = 0.1372 |
| A5 | 0.4588 * 0.3 = 0.1376 |
0.5893 * 0.2 = 0.1179 |
0.4932 * 0.2 = 0.0986 |
0.305 * 0.3 = 0.0915 |
#04 Solusi Ideal
Perhitungan solusi ideal sesuai dengan atribut masing-masing kriteria yaitu:
- Kriteria Tanggungan (
benefit)
Solusi Ideal Positif = max(0.1721, 0.1721, 0.0344, 0.1032, 0.1376) =0.1721
Solusi Ideal Negatif = min(0.1721, 0.1721, 0.0344, 0.1032, 0.1376) =0.0344 - Kriteria IPK (
benefit)
Solusi Ideal Positif = max(0.0707, 0.1179, 0.0471, 0.0707, 0.1179) =0.1179
Solusi Ideal Negatif = min(0.0707, 0.1179, 0.0471, 0.0707, 0.1179) =0.0471 - Kriteria Semester (
benefit)
Solusi Ideal Positif = max(0.0986, 0.0986, 0.0986, 0.0329, 0.0986) =0.0986
Solusi Ideal Negatif = min(0.0986, 0.0986, 0.0986, 0.0329, 0.0986) =0.0329 - Kriteria Penghasilan Orang Tua (
cost)
Solusi Ideal Positif = min(0.0915, 0.2287, 0.0457, 0.1372, 0.0915) =0.0457
Solusi Ideal Negatif = max(0.0915, 0.2287, 0.0457, 0.1372, 0.0915) =0.2287
#05 Jarak Solusi Ideal
Tahap pertama dalam menghitung jarak solusi ideal adalah dengan mengkuadratkan selisih matriks normalisasi terbobot dengan solusi ideal positif dan negatif:
Jarak Solusi Ideal Positif
| Kode | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| A1 | (0.1721 - 0.1721)^2 = 0 |
(0.0707 - 0.1179)^2 = 0.0022 |
(0.0986 - 0.0986)^2 = 0 |
(0.0915 - 0.0457)^2 = 0.0021 |
| A2 | (0.1721 - 0.1721)^2 = 0 |
(0.1179 - 0.1179)^2 = 0 |
(0.0986 - 0.0986)^2 = 0 |
(0.2287 - 0.0457)^2 = 0.0335 |
| A3 | (0.0344 - 0.1721)^2 = 0.0189 |
(0.0471 - 0.1179)^2 = 0.005 |
(0.0986 - 0.0986)^2 = 0 |
(0.0457 - 0.0457)^2 = 0 |
| A4 | (0.1032 - 0.1721)^2 = 0.0047 |
(0.0707 - 0.1179)^2 = 0.0022 |
(0.0329 - 0.0986)^2 = 0.0043 |
(0.1372 - 0.0457)^2 = 0.0084 |
| A5 | (0.1376 - 0.1721)^2 = 0.0012 |
(0.1179 - 0.1179)^2 = 0 |
(0.0986 - 0.0986)^2 = 0 |
(0.0915 - 0.0457)^2 = 0.0021 |
Jarak Solusi Ideal Negatif
| Kode | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| A1 | (0.1721 - 0.0344)^2 = 0.0189 |
(0.0707 - 0.0471)^2 = 0.0006 |
(0.0986 - 0.0329)^2 = 0.0043 |
(0.0915 - 0.2287)^2 = 0.0188 |
| A2 | (0.1721 - 0.0344)^2 = 0.0189 |
(0.1179 - 0.0471)^2 = 0.005 |
(0.0986 - 0.0329)^2 = 0.0043 |
(0.2287 - 0.2287)^2 = 0 |
| A3 | (0.0344 - 0.0344)^2 = 0 |
(0.0471 - 0.0471)^2 = 0 |
(0.0986 - 0.0329)^2 = 0.0043 |
(0.0457 - 0.2287)^2 = 0.0335 |
| A4 | (0.1032 - 0.0344)^2 = 0.0047 |
(0.0707 - 0.0471)^2 = 0.0006 |
(0.0329 - 0.0329)^2 = 0 |
(0.1372 - 0.2287)^2 = 0.0084 |
| A5 | (0.1376 - 0.0344)^2 = 0.0107 |
(0.1179 - 0.0471)^2 = 0.005 |
(0.0986 - 0.0329)^2 = 0.0043 |
(0.0915 - 0.2287)^2 = 0.0188 |
Tahap kedua adalah dalam menghitung jarak solusi ideal adalah mengakarkan total nilai tabel di atas (positif dan nehatif) untuk setiap alternatif. Hasil dan perhitungannya bisa dilihat di tabel berikut:
| Kode | Positif | Negatif |
|---|---|---|
| A1 | \( \sqrt{0+0.0022+0+0.0021} \) = 0.0657 |
\( \sqrt{0.0189+0.0006+0.0043+0.0188} \) = 0.2066 |
| A2 | \( \sqrt{0+0+0+0.0335} \) = 0.183 |
\( \sqrt{0.0189+0.005+0.0043+0} \) = 0.1681 |
| A3 | \( \sqrt{0.0189+0.005+0+0} \) = 0.1547 |
\( \sqrt{0+0+0.0043+0.0335} \) = 0.1945 |
| A4 | \( \sqrt{0.0047+0.0022+0.0043+0.0084} \) = 0.1402 |
\( \sqrt{0.0047+0.0006+0+0.0084} \) = 0.1169 |
| A5 | \( \sqrt{0.0012+0+0+0.0021} \) = 0.0572 |
\( \sqrt{0.0107+0.005+0.0043+0.0188} \) = 0.197 |
#06 Nilai Preferensi
Perhitungan nilai preferensi berdasarkan jarak solusi ideal positif dan negatif, yaitu:
| Kode | Perhitungan | Hasil |
|---|---|---|
| A1 | 0.2066/( 0.2066 + 0.0657) | 0.7587 |
| A2 | 0.1681/( 0.1681 + 0.183) | 0.4788 |
| A3 | 0.1945/( 0.1945 + 0.1547) | 0.5569 |
| A4 | 0.1169/( 0.1169 + 0.1402) | 0.4547 |
| A5 | 0.197/( 0.197 + 0.0572) | 0.7749 |
#07 Perangkingan
Perangkingan berdasarkan nilai preferensi yang terbesar.
| Rank | Kode | Nama | Preferensi |
|---|---|---|---|
| 1 | A5 | Christina | 0.7749 |
| 2 | A1 | Maria | 0.7587 |
| 3 | A3 | Antonio | 0.5569 |
| 4 | A2 | Ana | 0.4788 |
| 5 | A4 | Thomas | 0.4547 |
Berdasarkan perhitungan metode TOPSIS di atas, maka alternatif yang terpilih adalah Christina dengan total nilai 0.7749
Perhitungan TOPSIS dengan Microsoft Excel
Buat data matriks evaluasi di sel A2:E7.
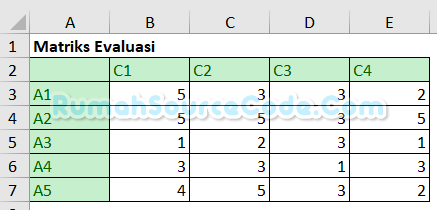
Buat rumus =B3^2 di sel B11 untuk mengkuadratkan matriks evaluasi.

Buat rumus =B3/SQRT(SUM(B$11:B$15)) di sel B19 untuk mencari normalisasi
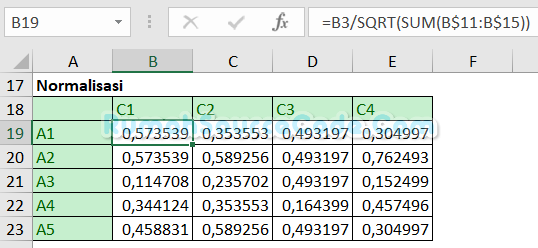
Isikan bobot kriteria di sel B27:E27. Buat rumus =B19*B$27/SUM($B$27:$E$27) di sel B28 untuk mencari normalisasi terbobot.
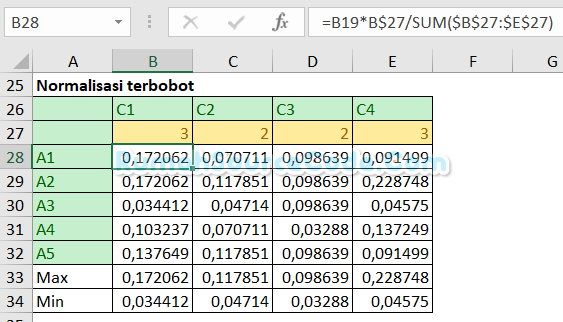
Max di cell B33 isi dengan rumus =MAX(B28:B32). Min di cell B34 isi dengan rumus =MIN(B28:B32)
Isikan atribut kriteria di sel B38:E38. Buat rumus =IF(B38="benefit";B33;B34) di sel B39 untuk mencari solusi ideal positif. Buat rumus =IF(B38="cost";B33;B34) di sel B40 untuk mencari solusi ideal negatif.
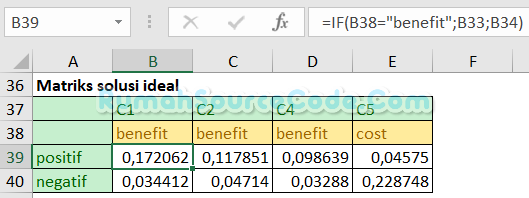
Buat rumus =(B28-B$39)^2 di sel B44 untuk menghitung matriks solusi ideal positif.
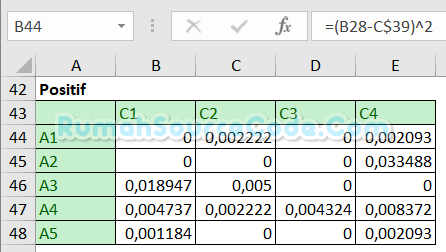
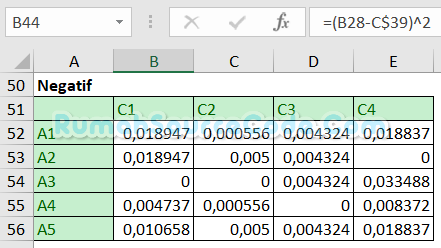
Buat rumus =(B28-B$40)^2 di sel B52 untuk menghitung matriks solusi ideal negatif.

Buat rumus =SQRT(SUM(B44:E44)) di sel B60 untuk menghitung total jarak positif. Buat rumus =SQRT(SUM(B52:E52)) di sel C60 untuk menghitung total jarak negatif. Buat rumus =C60/(B60+C60) di sel D60 untuk menghitung nilai preferensi. Buat rumus =RANK(D60;$D$60:$D$64) di sel E60 untuk menentukan peringkat.
Database TOPSIS
Kita perlu tiga tabel untuk membuat database TOPSIS yaitu: Alternatif, Kriteria, dan Nilai.
Tabel Alternatif tb_alternatif
Struktur tabel:
| Atribut | Tipe | Ket |
|---|---|---|
| kode_alternatif | varchar(16) | Primary Key |
| nama_alternatif | varchar(255) |
Sintaks SQL:
CREATE TABLE tb_alternatif ( kode_alternatif varchar(16) NOT NULL, nama_alternatif varchar(255) DEFAULT NULL, PRIMARY KEY (kode_alternatif) )
Tabel Kriteria tb_kriteria
Struktur tabel:
| Atribut | Tipe | Ket |
|---|---|---|
| kode_kriteria | varchar(16) | Primary Key |
| nama_kriteria | varchar(255) | |
| atribut | varchar(16) | |
| bobot | double |
Sintaks SQL:
CREATE TABLE tb_kriteria ( kode_kriteria varchar(16) NOT NULL, nama_kriteria varchar(255) DEFAULT NULL, atribut varchar(16) DEFAULT NULL, bobot double DEFAULT NULL, PRIMARY KEY (kode_kriteria) )
Tabel Nilai tb_rel_alternatif
Struktur tabel:
| Atribut | Tipe | Ket |
|---|---|---|
| kode_alternatif | varchar(16) | |
| kode_kriteria | varchar(16) | |
| nilai | double |
Sintaks SQL:
CREATE TABLE tb_rel_alternatif ( kode_alternatif varchar(16) DEFAULT NULL, kode_kriteria varchar(16) DEFAULT NULL, nilai double DEFAULT NULL )
Entity Relationship Diagram
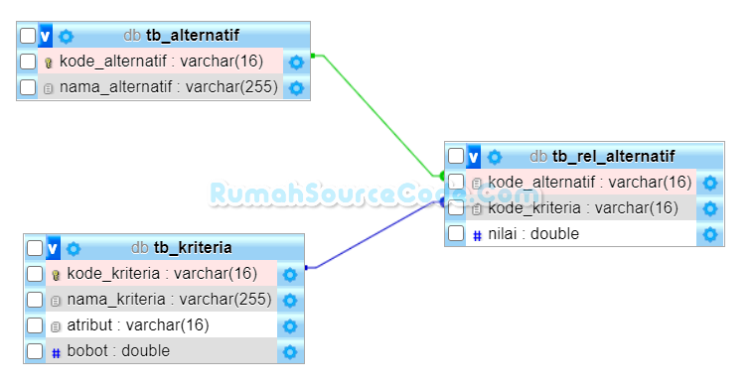
tb_alternatif berelasi one to many ke tb_rel_alternatif, begitu juga tb_kriteria berelasi one to many ke tb_rel_alternatif.
Source Code Metode TOPSIS
Berikut adalah beberapa source-code yang menggunakan metode TOPSIS baik berbasis web maupun desktop.
- Source Code SPK Metode TOPSIS Periode Codeigniter
- Source Code SPK Metode TOPSIS PHP
- Source Code SPK Metode AHP TOPSIS PHP
- Source Code SPK Metode TOPSIS Codeigniter
- Source Code SPK Metode TOPSIS VB.Net
- Source Code SPK Metode TOPSIS Laravel
- Source Code SPK Metode TOPSIS C Sharp (C#)
- Source Code SPK Metode Fuzzy AHP TOPSIS PHP
- Source Code SPK Metode AHP TOPSIS C#
- Source Code SPK Metode AHP TOPSIS Laravel
- Source Code SPK Metode Gabungan SAW TOPSIS PHP
- Source Code SPK Metode Fuzzy C Means TOPSIS PHP
- Source Code Penjurusan Metode TOPSIS PHP
- Source Code Rekomendasi Metode TOPSIS PHP
- Source Code SPK Metode TOPSIS Periode PHP
- Source Code SPK Metode TOPSIS GIS PHP
- Source Code SPK Metode Fuzzy TOPSIS PHP
- Source Code SPK Metode AHP TOPSIS CodeIgniter
- Source Code SPK Metode AHP MOORA TOPSIS PHP
- Source Code Penjurusan Metode Profile Matching TOPSIS Laravel
Referensi
Ada yang Ditanyakan?
Jika anda masih ada kesulitan atau kekeliruan tentang penjelasan metode di atas, bisa menghubungi kami lewat WA/Email sesuai halaman Kontak.
Jika ingin memiliki file excel dari metode di atas bisa melihat cara download di halaman Download.
Jika ingin memiliki source code dari metode di atas, baik berbasis web maupun desktop bisa melihat daftar harga donasi di halaman Daftar Source Code.
Donasi ini digunakan oleh penulis untuk membayar server dan membeli kopi sembari membuat tutorial Metode/Algoritma lainnya :).
PENCARIAN
PRODUK POPULER
Source Code Text Mining Metode Naive Bayes Classifier PHP
Source Code Text Mining Metode Naive Bayes Clasifier PHP, Kasus Sentimen, Kasus Skripsi, Kasus Hoax.
Source Code Sistem Informasi Akuntansi Koperasi Simpan Pinjam Laravel
Source Code Sistem Informasi Akuntansi Koperasi Simpan Pinjam Berbais Web Laravel, SHU, Pinjaman, Simpanan, Laba Rugi, Neraca
Source Code SPK Metode AHP Codeigniter + Crisp
Source code sistem pendukung keputusan (SPK) metode Analytical Hierarkhi Process (AHP) berbasis web dengan Codeigniter dan MySQL dengan Crisp.
Source Code Sistem Pakar Metode Naive Bayes Classifier VB
Source Code Sistem Pakar Metode Naive Bayes Classifier dengan VB.Net dan Microsoft Access.
Source Code SPK Metode AHP MOORA PHP + Periode
Source code SPK (Sistem Pendukung Keputusan) metode AHP (Analitical Hierarchy Process) MOORA (Multi-Objective Optimization on the basic of Ratio Analysis) + Periode dengan PHP dan MySQL.




